On the effects of locking weasels [updated]

For those of you new to the discussion the bright-lights of the ID movement seem to think Richard Dawkins' toy example of the power of random variation and selection, a program that 'evolves' Hamlet's mocking line to Polonius "Methinks it is like a weasel", is a bit of a cheat because it fixes correct letters in place once they match the target string. This is not true. If you want to follow the whole story Ian Musgrave is your man.

Just for fun I thought I look at how, and when, the 'locking' approach than the IDers think Dawkins used gets you the target phrase more quickly. Below is the result of 100 runs of the weasel program with and without locking and with various parameters

Effect of 'locking' on number of generations required to evolve target phrase

What you see above is the net result of pairs of "unlocked" and "locked" runs at different population sizes (n) and mutation rates (u). When the population in each generation is 100 and the chance of each character mutating is 0.01 there is a small (but significant) difference in number of generations required to get to the target. Up the mutation rate to 0.1 and the locking method comes into its own, with correct bases protected from the threat of deleterious mutations (which become much more likely as the "best" sting approaches the target) and mutations are effectively targeted to areas in which they are needed. Locked and unlocked programs are no longer significantly different when the population size is brought up to 1000 (since one of those 1000 strings is likely to have a beneficial mutation and retain all it's correct letters).

So, when the mutation rate is high 'locking' greatly speeds up the evolution of the target string by protecting the characters that are already matching and when population size is high it doesn't make much difference because both approaches will likely find a 'fitter' string that retains the matching characters of the parent.

So, at what mutation rates is the differences between the locking and non-locking approaches most stark, it's easy enough to run the weasel program at a bunch of different mutation rates:

The effect of Mutation Rate on generations required for locking and non-locking programs to converge on target string

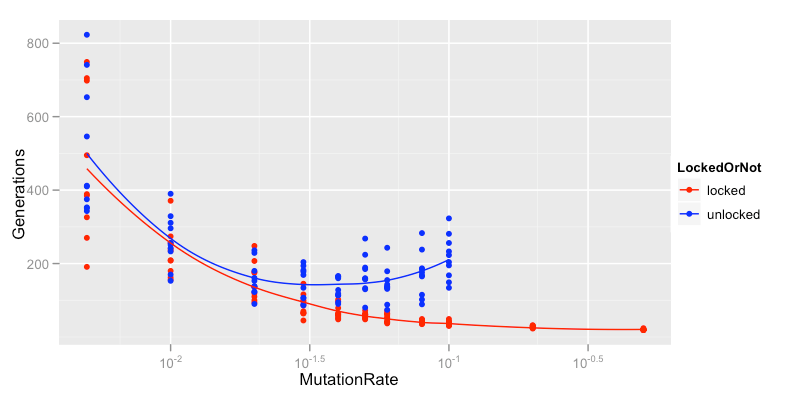
All these runs have a population size of 100. As you can see the locking approach is always quicker than the unlocked one but while the mutation rate is less than about 0.03 (3/popsize in this case) they are very similar. Once you raise the mutation rate above about 0.05 the unlocked mechanism actually gets slower as matching bases go unprotected against the the onslaught of mutation. This effect becomes so strong that for mutation rates above 0.1 the the algorithm can actually lose ground in its search for the target string:

Fitness of "best match" in one run of the weasel algorithm n = 100 u = 0.2

So, what have we learned from all this? The cumulative selection displayed in the "unlocked" weasel algorithm can certainly generate sentences that "blind chance" wouldn't arrive at during the lifetime of the universe. The 'locked' version of of the program that Dembski et al think Dawkins used is faster than the unlocked one but difference is trivial with relatively large population sizes and small mutation rates. All stuff that you could probably have worked out in first principles and took a dilettante programmer a few hours of spare time to show. Oh, and that the Evolutionary Informatics Lab still hasn't actually, you know, tried to test the things Dembski's been saying...

Labels: creationism, Dawkins, mutation, python, sci-blogs, weasel

0 Comments:

Post a Comment

All content not otherwise marked is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.